# 经典排序算法

快速排序，堆排序

6. 快速排序
7. 堆排序

# 6. 快速排序

快速排序(Quick Sort)又是一种分而治之思想在排序算法上的典型应用，本质上来看，快速排序应该算是在冒泡排序基础上的递归分治法

通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序

# 6.1. 算法步骤

从数列中挑出一个元素，称为轴（基准）(pivot)
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边，不稳定的），在这个分区退出之后，该基准就处于数列的中间位置，这个称为分区(partition)操作
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了，虽然一直递归下去，但是这个算法总会退出，因为在每次的迭代(iteration)中，它至少会把一个元素摆到它最后的位置去

# 6.2. 选取基准

从数列中挑出一个轴（基准）(pivot)涉及到三种处理方式

首尾元素
随机选取
三数取中法

首尾元素

这种选取基准值的方法在整个数列已经趋于有序的情况下，效率很低，比如有序序列，当我们选取 0 为基准值的时候，需要将后面的元素每个都交换一遍，效率很低，所以这种以固定位置选取基准值的方式，只适用于该序列本身并不是趋于有序的情况下，比如一串随机数列，此时的效率还能够差强人意

随机选取

引入随机化快速排序的作用，就是当该序列趋于有序时，能够让效率提高，大量的测试结果证明，该方法确实能够提高效率

三数取中法

取首中尾三个数中间大的那个数，采用三数取中法很好的解决了很多特殊的问题，但对于很多重复的序列，效果依然不好。于是在这三种选取基准值的方法下，另外地还有三种优化方法

当待排序序列的长度分割到一定大小后，使用插入排序，比如元素小于 10
在一次排序后，可以将与基准值相等的数放在一起，在下次分割时可以不考虑这些数
优化递归操作

# 6.3. 算法分析

而在分区处理中，又会有多种不同的处理方式

单轴
- 单路
  - 前后指针法，也叫快慢指针法
- 双路
  - 交换法(Hoare)
  - 挖坑法
- 三路
双轴
- 三路
- 五路

# 6.3.1. 单轴单路

在有较多重复元素的时候，会造成左右分配不平衡的问题，可能会退化成 O(n^2) 级别的排序，如下代码片段

/**
 * 代码片段，详细查看 6.7. 前后指针法
 */
private int partition(int[] arr, int left, int right) {
    int pivot = left;
    int index = pivot + 1;
    for (int i = index; i <= right; i++) {
        if (arr[i] < arr[pivot]) {
            swap(arr, i, index);
            index++;
        }
    }
    swap(arr, pivot, index - 1);
    return index - 1;
}

# 6.3.2. 单轴双路

单轴双路快速排序算法，最为经典的快排，partition 过程使用两个索引值(i、j)用来遍历数组，将小于 pivot 的元素放在索引 i 所指向位置的左边，而将大于 pivot 的元素放在索引 j 所指向位置的右边

// 分为如下两个区
| 小于 pivot 的元素 | 大于 pivot 的元素 |

交换法(Hoare)

/**
 * 代码片段，详细查看 6.6. 基础版本
 */
private static int partition(int[] array, int left, int right) {
    int pivot = left;
    int i = pivot + 1, j = right;
    while (i <= j) {
        while (i <= j && array[i] <= array[pivot]) {
            i++;
        }
        while (i <= j && array[j] >= array[pivot]) {
            j--;
        }
        if (i <= j) {
            int temp = array[i];
            array[i] = array[j];
            array[j] = temp;
        }
    }
    int temp = array[left];
    array[left] = array[j];
    array[j] = temp;
    return j;
}

挖坑法

/**
 * 代码片段，详细查看 6.8. 挖坑法
 */
private static int partition(int[] array, int left, int right) {
    int pivot = array[left];
    int i = left, j = right;
    while (i < j) {
        while (i <= j && array[j] > pivot) {
            j--;
        }
        if (i < j) {
            array[i] = array[j];
            i++;
        }
        while (i <= j && array[i] <= pivot) {
            i++;
        }
        if (i < j) {
            array[j] = array[i];
            j--;
        }
    }
    array[j] = pivot;
    return j;
}

# 6.3.3. 单轴三路

比双路快排多考虑一个与被对比元素相等的情况，在完全随机且 left - right 较大的情况下，会比双路慢一点（因为多一个判断），但在有大量相同的元素的情况下，速度很快

// 分为如下三个区
| 小于 pivot  | 等于 pivot  | 大于 pivot |

# 6.3.4. 双轴三路

双轴快排(Dual Pivot Quick Sort)，同时选取两个轴（基准）(pivot)，Java 数组底层排序就是使用的双轴

// 分为如下三个区
| 小于 pivot1 | 大于 pivot1 小于 pivot2 | 大于 pivot2 |

# 6.3.5. 双轴五路

// 分为如下五个区
| 小于 pivot1 | 等于 pivot1 | 大于 pivot1 小于 pivot2 | 等于 pivot2 | 大于 pivot2 |

# 6.4. 一轮排序

先写出一轮的快速排序处理，这里是单轴双路快速排序，使用交换法(Hoare)，首元素为轴

/**
 * 先写出一轮的快速排序处理
 * 设定 pivot = 0 的轴进行快排
 *
 * 从左边开始，找到一个小于pivot的数
 * 从右边开始，找到有个大于pivot的数
 * 然后进行交换，输出可以看到，数据进行了两组交换
 *
 * @param array
 */
private static void quickSort1(int[] array) {
    print(array);

    // 设定 pivot = 0 的轴进行快排
    int pivot = 0;
    int left = pivot + 1, right = array.length - 1;

    while (left <= right) {
        while (left <= right && array[left] <= array[pivot]) {
            left++;
        }
        while (left <= right && array[right] >= array[pivot]) {
            right--;
        }
        if (left <= right) {
            int temp = array[left];
            array[left] = array[right];
            array[right] = temp;

            // System.out.println("left " + left + " right " + right);
            print(array);
        }
    }

    // System.out.println("left " + left + " right " + right);
    // 交换轴，右下标是比轴小的数据，所以轴和右下标交换
    int temp = array[pivot];
    array[pivot] = array[right];
    array[right] = temp;

    print(array);
}

给定一个数组输出，可以看到数据进行了两组交换，7 1，9 2

public static void main(String[] args) {
    int[] array = {5, 3, 7, 9, 4, 8, 2, 6, 1};
    System.out.println("---------- quickSort1 ----------");
    quickSort1(Arrays.copyOf(array, array.length));
}

---------- quickSort1 ----------
5 3 7 9 4 8 2 6 1 
5 3 1 9 4 8 2 6 7 
5 3 1 2 4 8 9 6 7 
4 3 1 2 5 8 9 6 7

# 6.5. 抽取方法

抽取分区方法，这里是单轴双路快速排序，使用交换法(Hoare)，首元素为轴

/**
 * 抽取公共方法
 *
 * @param array
 */
private static void quickSort2(int[] array) {
    print(array);

    int partitionIndex = partition(array, 0, array.length - 1);
    // System.out.println("partitionIndex " + partitionIndex);

    // print(array);
}

/**
 * 抽取方法
 *
 * @param array
 * @param left
 * @param right
 * @return
 */
private static int partition(int[] array, int left, int right) {
    int pivot = left;
    int i = pivot + 1, j = right;

    while (i <= j) {
        while (i <= j && array[i] <= array[pivot]) {
            i++;
        }
        while (i <= j && array[j] >= array[pivot]) {
            j--;
        }
        if (i <= j) {
            int temp = array[i];
            array[i] = array[j];
            array[j] = temp;

            // System.out.println("i " + i + " j " + j);
            print(array);
        }
    }

    // System.out.println("s i " + i + " j " + j);

    // 交换轴，右下标是比轴小的数据，所以轴和右下标交换
    int temp = array[left];
    array[left] = array[j];
    array[j] = temp;

    print(array);

    return j;
}

给定一个数组输出，可以看到数据也进行了两组交换，方法抽取成功

public static void main(String[] args) {
    int[] array = {5, 3, 7, 9, 4, 8, 2, 6, 1};
    System.out.println("---------- quickSort2 ----------");
    quickSort2(Arrays.copyOf(array, array.length));
}

---------- quickSort2 ----------
5 3 7 9 4 8 2 6 1 
5 3 1 9 4 8 2 6 7 
5 3 1 2 4 8 9 6 7 
4 3 1 2 5 8 9 6 7

# 6.6. 基础版本

加上递归，基础版本完成，这里是单轴双路快速排序，使用交换法(Hoare)，首元素为轴

/**
 * 递归处理，基础版本
 *
 * @param array
 */
private static void quickSort3(int[] array) {
    print(array);

    sort(array, 0, array.length - 1);

    // print(array);
}

/**
 * 递归方法
 *
 * @param array
 * @param left
 * @param right
 */
private static void sort(int[] array, int left, int right) {
    if (left >= right) {
        return;
    }

    int partitionIndex = partition(array, left, right);
    // System.out.println("left " + left + " right " + right + " partitionIndex " + partitionIndex);
    sort(array, left, partitionIndex - 1);
    sort(array, partitionIndex + 1, right);
}

给定一个数组输出，可以看到排序成功

public static void main(String[] args) {
    int[] array = {5, 3, 7, 9, 4, 8, 2, 6, 1};
    System.out.println("---------- quickSort3 ----------");
    quickSort3(Arrays.copyOf(array, array.length));
}

---------- quickSort3 ----------
5 3 7 9 4 8 2 6 1 
5 3 1 9 4 8 2 6 7 
5 3 1 2 4 8 9 6 7 
4 3 1 2 5 8 9 6 7 
2 3 1 4 5 8 9 6 7 
2 1 3 4 5 8 9 6 7 
1 2 3 4 5 8 9 6 7 
1 2 3 4 5 8 7 6 9 
1 2 3 4 5 6 7 8 9 
1 2 3 4 5 6 7 8 9

# 6.7. 前后指针法

前后指针法动图演示

/**
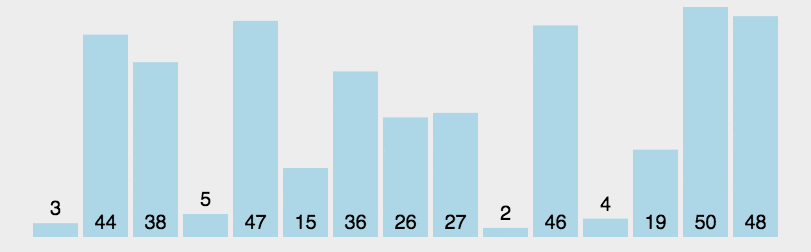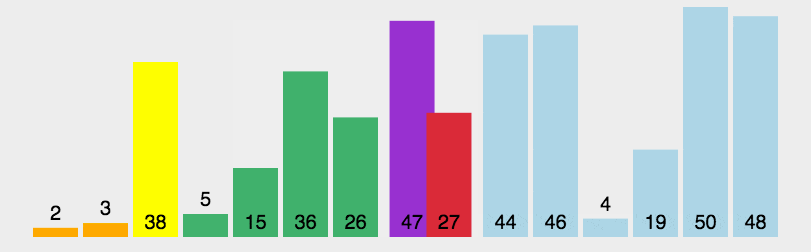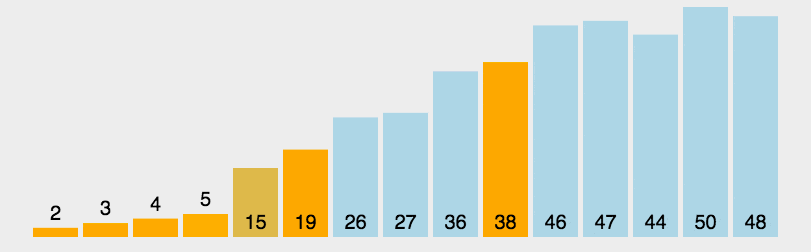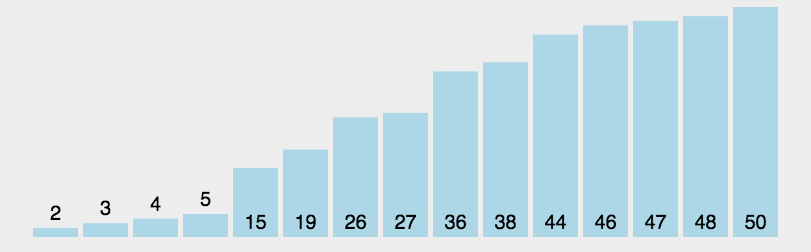
 * 单轴单路快速排序，前后指针法，pivot 这里采用首元素
 *
 * @author wliduo[i@dolyw.com]
 * @date 2022/11/28 9:52
 */
public class QuickSort2 {

    /**
     * 快速排序算法
     *
     * @param args
     */
    public static void main(String[] args) {
        int[] array = {5, 3, 7, 9, 4, 8, 2, 6, 1};

        System.out.println("---------- quickSort3 ----------");
        quickSort3(Arrays.copyOf(array, array.length));
    }

    /**
     * 抽取方法
     * 单轴单路快速排序，前后指针法，pivot 这里采用首元素
     *
     * @param array
     * @param left
     * @param right
     * @return
     */
    private static int partition(int[] array, int left, int right) {
        int pivot = left;
        int index = pivot + 1;
        for (int i = index; i <= right; i++) {
            if (array[i] < array[pivot]) {
                int temp = array[i];
                array[i] = array[index];
                array[index] = temp;
                index++;
            }
        }
        int temp = array[pivot];
        array[pivot] = array[index - 1];
        array[index - 1] = temp;
        print(array);
        return index - 1;
    }

    /**
     * 递归处理，基础版本
     *
     * @param array
     */
    private static void quickSort3(int[] array) {
        print(array);

        sort(array, 0, array.length - 1);

        // print(array);
    }

    /**
     * 递归方法
     *
     * @param array
     * @param left
     * @param right
     */
    private static void sort(int[] array, int left, int right) {
        if (left >= right) {
            return;
        }

        int partitionIndex = partition(array, left, right);
        // System.out.println("left " + left + " right " + right + " partitionIndex " + partitionIndex);
        sort(array, left, partitionIndex - 1);
        sort(array, partitionIndex + 1, right);

    }

    /**
     * 打印数组
     *
     * @param array
     */
    private static void print(int[] array) {
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + " ");
        }
        System.out.println();
    }
}

# 6.8. 挖坑法

/**
 * 单轴双路快速排序，挖坑法，pivot 这里采用首元素
 *
 * @author wliduo[i@dolyw.com]
 * @date 2022/11/28 9:52
 */
public class QuickSort3 {

    /**
     * 快速排序算法
     *
     * @param args
     */
    public static void main(String[] args) {
        int[] array = {5, 3, 7, 9, 4, 8, 2, 6, 1};

        System.out.println("---------- quickSort3 ----------");
        quickSort3(Arrays.copyOf(array, array.length));
    }

    /**
     * 抽取方法
     * 单轴双路快速排序，挖坑法，pivot 这里采用首元素
     *
     * @param array
     * @param left
     * @param right
     * @return
     */
    private static int partition(int[] array, int left, int right) {
        int pivot = array[left];
        int i = left, j = right;

        while (i < j) {
            // 从右向左找出比pivot小的数据
            while (i <= j && array[j] > pivot) {
                j--;
            }
            // 找到后立即放入左边坑中，当前位置变为新的"坑"
            if (i < j) {
                array[i] = array[j];
                i++;
            }
            // 从左向右找出比pivot大的数据
            while (i <= j && array[i] <= pivot) {
                i++;
            }
            // 找到后立即放入右边坑中，当前位置变为新的"坑"
            if (i < j) {
                array[j] = array[i];
                j--;
            }
        }

        // System.out.println("s i " + i + " j " + j);

        // 将最开始存储的分界值放入当前的"坑"中
        array[j] = pivot;

        print(array);

        return j;
    }

    /**
     * 递归处理，基础版本
     *
     * @param array
     */
    private static void quickSort3(int[] array) {
        print(array);

        sort(array, 0, array.length - 1);

        // print(array);
    }

    /**
     * 递归方法
     *
     * @param array
     * @param left
     * @param right
     */
    private static void sort(int[] array, int left, int right) {
        if (left >= right) {
            return;
        }

        int partitionIndex = partition(array, left, right);
        // System.out.println("left " + left + " right " + right + " partitionIndex " + partitionIndex);
        sort(array, left, partitionIndex - 1);
        sort(array, partitionIndex + 1, right);

    }

    /**
     * 打印数组
     *
     * @param array
     */
    private static void print(int[] array) {
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + " ");
        }
        System.out.println();
    }
}

# 6.9. 算法总结

快速排序的平均运行时间是 O(n log n)，之所以特别快是由于非常精练和高度优化的内部循环，最坏的情形性能为 O(n^2)

从空间性能上看，快速排序只需要一个元素的辅助空间，但快速排序需要一个栈空间来实现递归，所以空间复杂度为 O(log n)

描述
- 小数，基准元素，大数
- 挑选一个元素作基准，将小于基准的元素放在基准前，大于基准的元素放在基准后，再分别对小数区与大数区进行排序
稳定性
- 不稳定
时间复杂度
- 最好是 O(n log n)
- 最差是 O(n^2)
- 所以平均复杂度为 O(n log n)
空间复杂度
- 占用额外空间，O(log n)

# 7. 堆排序

堆排序(Heap Sort)是指利用堆这种数据结构所设计的一种排序算法，堆排序可以说是一种利用堆的概念来排序的选择排序

# 7.1. 二叉树

一棵二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成

每个节点最多有两棵子树，即不存在超过度为 2 的节点
二叉树的子树有左右之分，且左右不能颠倒

完全二叉树

什么是满二叉树

如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树
如果一个二叉树的层数为 k，且结点总数是 (2^k) -1，则它就是满二叉树

完全二叉树是由满二叉树引出的

满二叉树要求每一层的节点数都达到最大值
完全二叉树仅要求除最后一层外的节点数达到最大值，也就是说最后一层可以不满
我们可以把满二叉树看成特殊的完全二叉树

二叉树的存储

顺序存储：一般数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费
链状存储：二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系

一般只有堆才会使用数组来存储

# 7.2. 堆(Heap)

堆是一种特殊的二叉树，具有一些特殊的性质

堆总是一棵完全二叉树
堆中某个子节点的键值或索引总是不大于（小于）其父节点的值

两种堆

我们把子节点都不大于父节点的称为大堆（大顶堆或大根堆），反之称为小堆（小顶堆或小根堆）

大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序中用于升序排列
小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序中用于降序排列

二叉树和堆详解 (opens new window)

# 7.3. 算法步骤

将待排序序列构建成一个堆 H[0……n-1]，根据（升序降序需求）选择大顶堆或小顶堆
把堆首（最大值）和堆尾互换
把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置
重复步骤 2，直到堆的尺寸为 1

# 7.4. 数组实现

/**
 * 堆排序 - 数组实现
 *
 * @author wliduo[i@dolyw.com]
 * @date 2022/12/01 10:03
 */
public class HeapSort {

    /**
     * 堆排序算法
     *
     * @param args
     */
    public static void main(String[] args) {
        int[] array = {10, 8, 12, 9, 5, 3, 7, 1, 6, 4, 2, 11};

        System.out.println("---------- heapSort ----------");

        print(array);

        int len = array.length;

        buildHeap(array, len);

        for (int i = len - 1; i > 0; i--) {
            int temp = array[0];
            array[0] = array[i];
            array[i] = temp;

            len--;
            heapify(array, 0, len);
        }

        print(array);
    }

    /**
     * 构建堆
     *
     * @param array
     * @param len
     */
    private static void buildHeap(int[] array, int len) {
        for (int i = (int) Math.floor(len / 2); i >= 0; i--) {
            heapify(array, i, len);
        }
    }

    /**
     * 堆调整
     *
     * @param array
     * @param i
     * @param len
     */
    private static void heapify(int[] array, int i, int len) {
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int largest = i;

        if (left < len && array[left] > array[largest]) {
            largest = left;
        }

        if (right < len && array[right] > array[largest]) {
            largest = right;
        }

        if (largest != i) {
            int temp = array[i];
            array[i] = array[largest];
            array[largest] = temp;

            heapify(array, largest, len);
        }
    }

    /**
     * 打印数组
     *
     * @param array
     */
    private static void print(int[] array) {
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + " ");
        }
        System.out.println();
    }
}

输出

---------- heapSort ----------
10 8 12 9 5 3 7 1 6 4 2 11 
1 2 3 4 5 6 7 8 9 10 11 12

# 7.5. PriorityQueue实现

import java.util.Comparator;
import java.util.PriorityQueue;

/**
 * 堆排序 - PriorityQueue实现
 *
 * PriorityQueue默认是一个小顶堆
 * 可以通过传入自定义的Comparator函数来实现大顶堆
 *
 * @author wliduo[i@dolyw.com]
 * @date 2022/12/01 10:03
 */
public class HeapSort2 {

    /**
     * 堆排序算法
     *
     * @param args
     */
    public static void main(String[] args) {
        int[] array = {10, 8, 12, 9, 5, 3, 7, 1, 6, 4, 2, 11};

        System.out.println("---------- heapSort ----------");

        print(array);

        // PriorityQueue<Integer> heap = new PriorityQueue<Integer>();
        // 创建大顶堆，默认小顶堆
        PriorityQueue<Integer> heap = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2 - o1;
            }
        });

        for (int i = 0; i < array.length; i++) {
            heap.offer(array[i]);
        }

        for (int i = 0; i < array.length; i++) {
            array[i] = heap.poll();
        }

        print(array);
    }

    /**
     * 打印数组
     *
     * @param array
     */
    private static void print(int[] array) {
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + " ");
        }
        System.out.println();
    }
}

输出

---------- heapSort ----------
10 8 12 9 5 3 7 1 6 4 2 11 
12 11 10 9 8 7 6 5 4 3 2 1

PriorityQueue的使用 (opens new window)

# 7.6. 算法总结

堆排序是一种利用堆的概念来排序的选择排序，所以也是不稳定的

描述
- 最大（小）堆，有序区
- 从堆顶把根卸出来放在有序区之前，再恢复堆
稳定性
- 不稳定
时间复杂度
- 最好是 O(n log n)
- 最差也是 O(n log n)
- 所以平均复杂度为 O(n log n)
空间复杂度
- 使用数组的话不占用额外空间，O(1)

参考

← 经典排序算法-03 经典排序算法-05 →