# 经典排序算法

希尔排序，归并排序

4. 希尔排序
5. 归并排序

# 4. 希尔排序

希尔排序(Shell Sort)，又称递减（缩小）增量排序，是插入排序的一种更高效的改进版本

希尔排序是基于插入排序的以下两点性质而提出改进方法的

插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率
但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位

它通过比较相距一定间隔的元素来进行，各趟比较所用的距离随着算法的进行而递减，直到只比较相邻元素的最后一趟排序为止

菜鸟教程 - 希尔排序 (opens new window)

增量计算方式

折半计算 array.length / 2，用序列 {n/2,(n/2)/2...1} 来表示
knuth 序列（克努特序列），h = 3*h + 1，(1,4,13,40,121...)
Hibbard增量，(1、3、7、15…)，通项公式为2^k-1，最坏的时间复杂度为 O(n^(3/2))
Sedgewick增量，(1、5、19、41、109…)，通项公式为 9 * 4^k - 9 * 2^k + 1 或者 4^k - 3 * 2^k + 1，最坏的时间复杂度为 O（n^(4/3)）

# 4.1. 算法步骤

先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序

选择一个增量序列 t1，t2，…，tk，其中 ti > tj，tk = 1
按增量序列个数 k，对序列进行 k 趟排序
每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序
仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度

# 4.2. 一轮排序

先局部后整体，先写第一轮排序流程是怎么处理的，再考虑整个流程

/**
 * 先写出第一轮排序，把插入复制过过来
 * 增加为12个数，按间隔，gap设定为4
 * 要改为 while (j - gap >= 0 大于等0，不然第一位数无法被排序
 *
 * 可以看到每4个间隔比较的数都进行了插入排序
 *
 * @param array
 */
private static void shellSort1(int[] array) {
    print(array);

    int gap = 4;

    // 从下标为 gap 开始，因为要和上一个 gap 比较，所以从 gap 开始
    for (int i = gap; i < array.length; i++) {
        int current = array[i];

        // 从后往前的开始比较，没有小于的数据后结束循环进行插入
        int j = i;
        while (j - gap >= 0 && (current < array[j - gap])) {
            array[j] = array[j - gap];
            j = j - gap;
        }

        // j和i不一致说明找到了比其小的数，进行插入
        if (j != i) {
            array[j] = current;
        }
    }

    print(array);
}

给定一个数组输出，可以看到每 4 个间隔的进行了排序，5 6 10，3 4 8等

public static void main(String[] args) {
    int[] array = {10, 8, 12, 9, 5, 3, 7, 1, 6, 4, 2, 11};
    System.out.println("---------- shellSort1 ----------");
    shellSort1(Arrays.copyOf(array, array.length));
}

---------- shellSort1 ----------
10 8 12 9 5 3 7 1 6  4 2  11 
5  3 2  1 6 4 7 9 10 8 12 11

# 4.3. 基础版本

增加外循环，在此我们选择常规折半计算 array.length / 2

/**
 * 基础版本，增加外循环，在此我们选择常规折半计算 array.length / 2
 * 递减增量以 gap = gap / 2 的方式，用序列 {n/2,(n/2)/2...1} 来表示
 *
 * while (j - gap >= 0 也相等于 j - gap > -1 也相等于 j > gap - 1
 *
 * @param array
 */
private static void shellSort2(int[] array) {
    print(array);

    for (int gap = array.length / 2; gap > 0; gap = gap / 2) {

        // 从下标为 gap 开始，因为要和上一个 gap 比较，所以从 gap 开始
        for (int i = gap; i < array.length; i++) {
            int current = array[i];

            // 从后往前的开始比较，没有小于的数据后结束循环进行插入
            int j = i;
            // while (j - gap >= 0 && (current < array[j - gap])) {
            while (j > gap - 1 && (current < array[j - gap])) {
                array[j] = array[j - gap];
                j = j - gap;
            }

            // j和i不一致说明找到了比其小的数，进行插入
            if (j != i) {
                array[j] = current;
            }
        }

        System.out.println(gap);
        print(array);
    }

    // print(array);
}

给定一个数组输出，可以看到每个间隔的输出，排序成功

public static void main(String[] args) {
    int[] array = {10, 8, 12, 9, 5, 3, 7, 1, 6, 4, 2, 11};
    System.out.println("---------- shellSort2 ----------");
    shellSort2(Arrays.copyOf(array, array.length));
}

---------- shellSort2 ----------
10 8 12 9 5 3 7  1 6  4  2  11 
6
7  1 6  4 2 3 10 8 12 9  5  11 
3
4  1 3  7 2 6 9  5 11 10 8  12 
1
1  2 3  4 5 6 7  8 9  10 11 12

# 4.4. 优化版本

使用 knuth 序列计算出对应的递减增量 gap，h = 3*h + 1

/**
 * 优化版本，使用 knuth 序列计算出对应的递减增量 gap，h = 3*h + 1
 *
 * @param array
 */
private static void shellSort3(int[] array) {
    print(array);

    // 计算增量
    int gap = 1;
    while (gap < array.length / 3) {
        gap = 3 * gap + 1;
    }

    while (gap > 0) {

        // 从下标为 gap 开始，因为要和上一个 gap 比较，所以从 gap 开始
        for (int i = gap; i < array.length; i++) {
            int current = array[i];

            // 从后往前的开始比较，没有小于的数据后结束循环进行插入
            int j = i;
            // while (j - gap >= 0 && (current < array[j - gap])) {
            while (j > gap - 1 && (current < array[j - gap])) {
                array[j] = array[j - gap];
                j = j - gap;
            }

            // j和i不一致说明找到了比其小的数，进行插入
            if (j != i) {
                array[j] = current;
            }
        }

        System.out.println(gap);
        print(array);

        // 重新计算增量
        gap = (gap - 1) / 3;
    }

    // print(array);
}

给定一个数组输出，可以看到每个间隔的输出，排序成功

public static void main(String[] args) {
    int[] array = {10, 8, 12, 9, 5, 3, 7, 1, 6, 4, 2, 11};
    System.out.println("---------- shellSort3 ----------");
    shellSort3(Arrays.copyOf(array, array.length));
}

---------- shellSort3 ----------
10 8 12 9 5 3 7 1 6  4  2  11 
4
5  3 2  1 6 4 7 9 10 8  12 11 
1
1  2 3  4 5 6 7 8 9  10 11 12

# 4.5. 算法总结

希尔排序对中等大小规模表现良好，但对规模非常大的数据排序不是最优选择，总之比一般 O(n^2 ) 复杂度的算法快得多

描述
- 每一轮按照事先决定的间隔进行插入排序，间隔会依次缩小，最后一次一定是 1
稳定性
- 不稳定的，增量间隔之间插入，可能存在相同的数交换位置
时间复杂度
- 最好是 O(n log n) or O(n^1.3)
- 最差是 O(n log^2 n) or O(n^2)
- 所以平均复杂度为 O(n log n) or O(n^1.3)
空间复杂度
- 没有占用额外空间，所以为常数阶 O(1)

# 5. 归并排序

归并排序(Merge Sort)是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法(Divide and Conquer)的一个非常典型的应用

将已有序的子序列合并，得到完全有序的序列，即先使每个子序列有序，再使子序列段间有序，若将两个有序表合并成一个有序表，称为二路归并，归并排序的实现两种方法

自上而下的递归（所有递归的方法都可以用迭代重写，所以就有了第 2 种方法）
自下而上的迭代

和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是 O(nlogn) 的时间复杂度，代价是需要额外的内存空间

# 5.1. 算法步骤

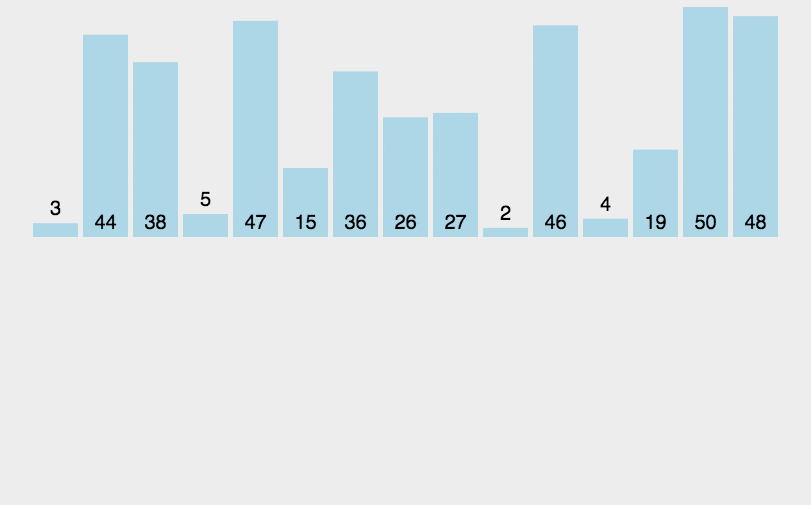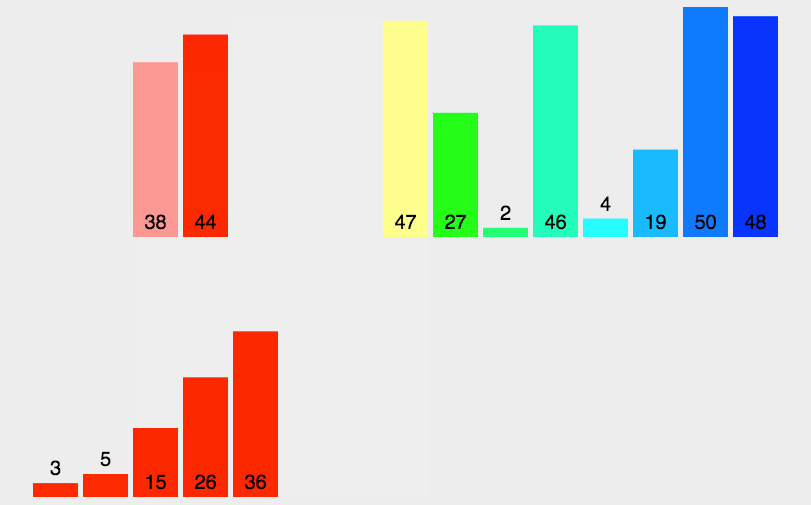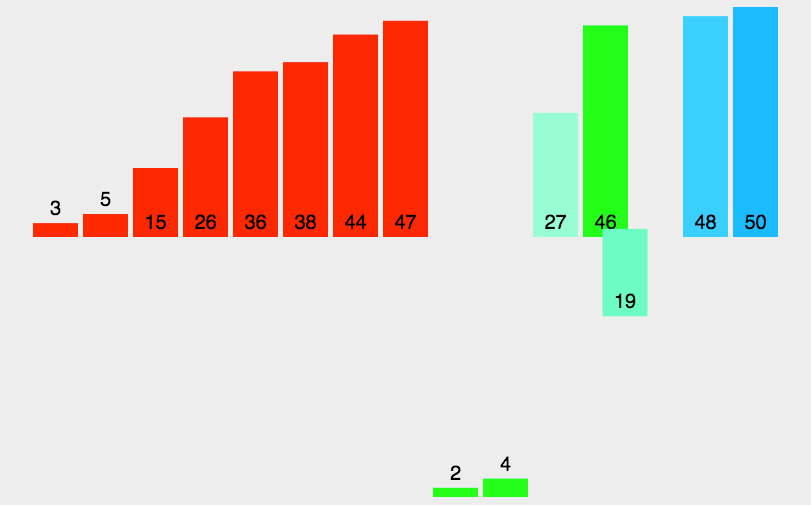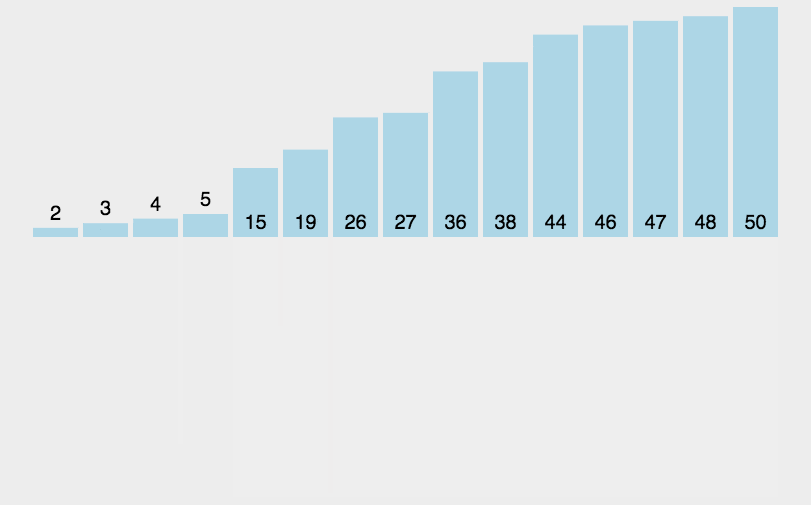
申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
设定两个指针，最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
重复步骤 3 直到某一指针达到序列尾
将另一序列剩下的所有元素直接复制到合并序列尾

简化

把长度为 n 的输入序列分成两个长度为 n/2 的子序列
对这两个子序列分别采用归并排序
将两个排序好的子序列合并成一个最终的排序序列

图解

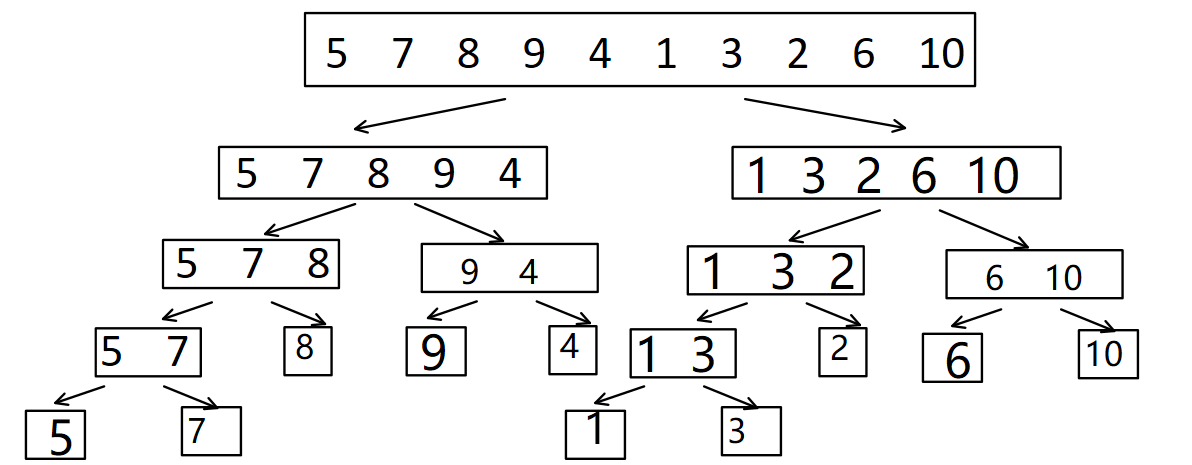
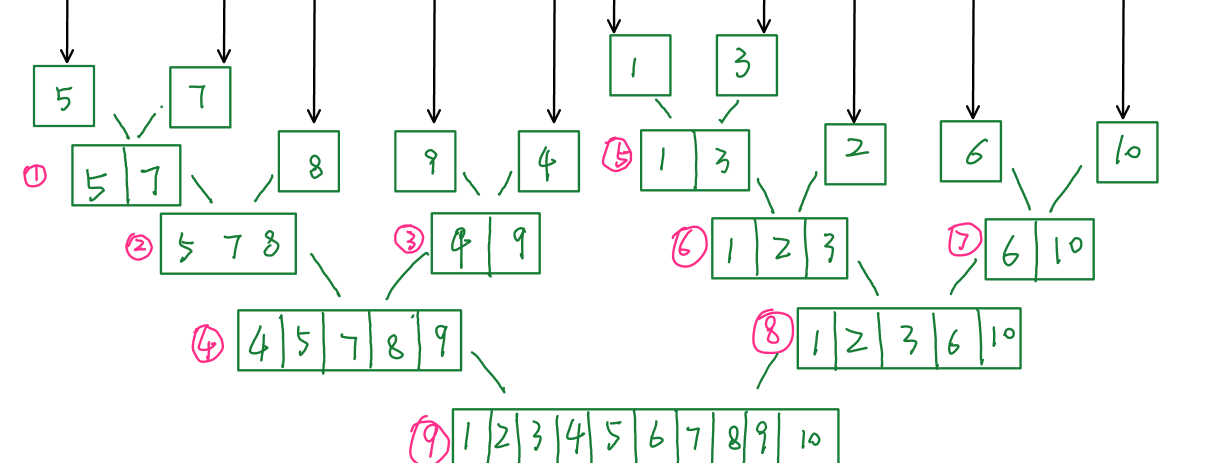
# 5.2. 一轮排序

先局部后整体，先写第一轮排序流程是怎么处理的，再考虑整个流程

/**
 * 先写出一轮的归并处理
 *
 * @param array
 */
private static void mergeSort1(int[] array) {
    print(array);

    // 计算中间位置
    int midIndex = array.length / 2;
    // 临时数组
    int[] tempArray = new int[array.length];

    int i = 0, j = midIndex + 1, k = 0;
    // j为中间位置+1，i和j对半进行比较，哪个小就放哪个
    while (i <= midIndex && j < array.length) {
        // <=，这样保证前面的和后面相等数，前面先下去，保证稳定性
        if (array[i] <= array[j]) {
            tempArray[k] = array[i];
            i++;
            k++;
        } else {
            tempArray[k] = array[j];
            j++;
            k++;
        }
    }
    // 对比完，多余剩下的数
    while (i <= midIndex) {
        tempArray[k] = array[i];
        i++;
        k++;
    }
    while (j < array.length) {
        tempArray[k] = array[j];
        j++;
        k++;
    }

    print(tempArray);
}

给定一个对半有序数组输出，可以看到进行一轮归并排序成功

public static void main(String[] args) {
    int[] array = {1, 3, 5, 7, 9, 2, 4, 6, 8};
    System.out.println("---------- mergeSort1 ----------");
    mergeSort1(Arrays.copyOf(array, array.length));
}

---------- mergeSort1 ----------
1 3 5 7 9 2 4 6 8 
1 2 3 4 5 6 7 8 9

# 5.3. 抽取方法

抽取归并方法，进行递归

/**
 * 抽取方法进行归并验证
 *
 * @param array
 */
private static void mergeSort2(int[] array) {

    print(array);

    // rightIndex 传 length - 1
    merge(array, 0, 2, 4);

    print(array);

    merge(array, 5, 6, 8);

    print(array);
}

/**
 * 抽取合并方法
 *
 * @param array
 * @param leftIndex
 * @param midIndex
 * @param rightIndex
 */
private static void merge(int[] array, int leftIndex, int midIndex, int rightIndex) {
    // 数组长度需要 + 1，因为 rightIndex 传的 length - 1
    int[] tempArray = new int[rightIndex + 1 - leftIndex];

    int i = leftIndex, j = midIndex + 1, k = 0;
    // j为中间位置+1，i和j对半进行比较，哪个小就放哪个
    while (i <= midIndex && j < rightIndex + 1) {
        // <=，这样保证前面的和后面相等数，前面先下去，保证稳定性
        if (array[i] <= array[j]) {
            tempArray[k++] = array[i++];
        } else {
            tempArray[k++] = array[j++];
        }
    }
    // 对比完，多余剩下的数
    while (i <= midIndex) {
        tempArray[k++] = array[i++];
    }
    while (j < rightIndex + 1) {
        tempArray[k++] = array[j++];
    }

    // 将结果赋值给原数组
    for (int m = 0; m < tempArray.length; m++) {
        array[leftIndex + m] = tempArray[m];
    }

    print(tempArray);

}

给定一个对半无序数组输出，可以看到对半的序列都排序成功

public static void main(String[] args) {
    int[] array2 = {3, 4, 5, 2, 7, 8, 9, 1, 6};
    System.out.println("---------- mergeSort2 ----------");
    mergeSort2(Arrays.copyOf(array2, array2.length));
}

---------- mergeSort2 ----------
3 4 5 2 7 8 9 1 6 
2 3 4 5 7 
2 3 4 5 7 8 9 1 6 
1 6 8 9 
2 3 4 5 7 1 6 8 9

# 5.4. 基础版本

再增加一个 sort 递归方法基础版本就完成了

/**
 * 基础版本，进行递归处理
 *
 * @param array
 */
private static void mergeSort3(int[] array) {

    print(array);

    sort(array, 0, array.length - 1);

    print(array);

    System.out.println("---------- analysis ----------");
    System.out.println("[5 3 2 9 4] [8 7 6 1]");
    System.out.println("[5 3 2] [9 4]");
    System.out.println("[5 3] [2]");
    System.out.println("[5] [3]");
    System.out.println("[9] [4]");
    System.out.println("[8 7] [6 1]");
    System.out.println("[8] [7]");
    System.out.println("[6] [1]");
}

/**
 * 递归方法
 *
 * @param array
 * @param leftIndex
 * @param rightIndex
 */
private static void sort(int[] array, int leftIndex, int rightIndex) {
    // System.out.println(leftIndex + "--" + rightIndex);
    if (leftIndex == rightIndex) {
        return;
    }

    // 两种都是一样的结果，计算两个下标的中间下标
    // int minIndex = (leftIndex + rightIndex) / 2;
    // 右下标减去左下标的差值的部分除以 2 得出差值的中间值，加左下标的部分得到总的中间下标
    int minIndex = leftIndex + (rightIndex - leftIndex) / 2;

    sort(array, leftIndex, minIndex);
    sort(array, minIndex + 1, rightIndex);

    merge(array, leftIndex, minIndex, rightIndex);
    // 优化版本，已经有序的两个数不进行重复归并
    /*if (array[minIndex] > (array[minIndex + 1])) {
        merge(array, leftIndex, minIndex, rightIndex);
    }*/
}

给定一个完全无序数组输出，可以看到排序成功

public static void main(String[] args) {
    int[] array3 = {5, 3, 2, 9, 4, 8, 7, 6, 1};
    System.out.println("---------- mergeSort3 ----------");
    mergeSort3(Arrays.copyOf(array3, array3.length));
}

---------- mergeSort3 ----------
5 3 2 9 4 8 7 6 1 
3 5 
2 3 5 
4 9 
2 3 4 5 9 
7 8 
1 6 
1 6 7 8 
1 2 3 4 5 6 7 8 9 
1 2 3 4 5 6 7 8 9 
---------- analysis ----------
[5 3 2 9 4] [8 7 6 1]
[5 3 2] [9 4]
[5 3] [2]
[5] [3]
[9] [4]
[8 7] [6 1]
[8] [7]
[6] [1]

# 5.5. 截取数组

还可以使用一种截取数组的方式实现归并排序，一轮排序修改如下

/**
 * 先写出一轮的归并处理
 *
 * @param array
 */
private static void mergeSort1(int[] array) {
    print(array);

    // 计算中间位置
    int midIndex = array.length / 2;
    // 临时数组
    int[] leftArray = Arrays.copyOfRange(array, 0, midIndex);
    int[] rightArray = Arrays.copyOfRange(array, midIndex, array.length);

    int[] tempArray = new int[leftArray.length + rightArray.length];

    int i = 0;
    while (leftArray.length > 0 && rightArray.length > 0) {
        if (leftArray[0] <= rightArray[0]) {
            tempArray[i++] = leftArray[0];
            leftArray = Arrays.copyOfRange(leftArray, 1, leftArray.length);
        } else {
            tempArray[i++] = rightArray[0];
            rightArray = Arrays.copyOfRange(rightArray, 1, rightArray.length);
        }
    }

    while (leftArray.length > 0) {
        tempArray[i++] = leftArray[0];
        leftArray = Arrays.copyOfRange(leftArray, 1, leftArray.length);
    }

    while (rightArray.length > 0) {
        tempArray[i++] = rightArray[0];
        rightArray = Arrays.copyOfRange(rightArray, 1, rightArray.length);
    }

    print(tempArray);
}

测试验证，输入输出没问题

int[] array = {1, 3, 5, 7, 2, 4, 6, 8, 9};

---------- mergeSort1 ----------
1 3 5 7 2 4 6 8 9 
1 2 3 4 5 6 7 8 9

基础版本修改如下

/**
 * 截取数组方式基础版本，归并排序
 *
 * @param array
 */
private static void mergeSort2(int[] array) {
    print(array);

    array = sort(array);

    print(array);
}

/**
 * 截取数组方式递归方法
 *
 * @param tempArray
 * @return
 */
private static int[] sort(int[] tempArray) {
    // print(tempArray);
    if (tempArray.length < 2) {
        return tempArray;
    }

    // 计算中间位置
    int midIndex = tempArray.length / 2;

    // System.out.println(midIndex);

    // 计算左右两个数组
    int[] leftArray = Arrays.copyOfRange(tempArray, 0, midIndex);
    int[] rightArray = Arrays.copyOfRange(tempArray, midIndex, tempArray.length);

    return merge(sort(leftArray), sort(rightArray));
}

/**
 * 截取数组方式归并方法
 *
 * @param leftArray
 * @param rightArray
 * @return
 */
private static int[] merge(int[] leftArray, int[] rightArray) {
    int[] tempArray = new int[leftArray.length + rightArray.length];

    int i = 0;
    while (leftArray.length > 0 && rightArray.length > 0) {
        if (leftArray[0] <= rightArray[0]) {
            tempArray[i++] = leftArray[0];
            leftArray = Arrays.copyOfRange(leftArray, 1, leftArray.length);
        } else {
            tempArray[i++] = rightArray[0];
            rightArray = Arrays.copyOfRange(rightArray, 1, rightArray.length);
        }
    }

    while (leftArray.length > 0) {
        tempArray[i++] = leftArray[0];
        leftArray = Arrays.copyOfRange(leftArray, 1, leftArray.length);
    }

    while (rightArray.length > 0) {
        tempArray[i++] = rightArray[0];
        rightArray = Arrays.copyOfRange(rightArray, 1, rightArray.length);
    }

    print(tempArray);
    return tempArray;
}

测试验证，输入输出没问题

int[] array2 = {5, 3, 2, 9, 4, 8, 7, 6, 1};

---------- mergeSort2 ----------
5 3 2 9 4 8 7 6 1 
3 5 
2 9 
2 3 5 9 
4 8 
1 6 
1 6 7 
1 4 6 7 8 
1 2 3 4 5 6 7 8 9 
1 2 3 4 5 6 7 8 9

# 5.6. 多路归并

上面使用的都是二路归并，还有多路归并实现的归并排序

待补充

# 5.7. 算法总结

归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是 O(nlogn) 的时间复杂度，代价是需要额外的内存空间

描述
- 把数据分为两段，从两段中逐个选最（大）小的元素移入新数据段的未尾
- 可从上到下或从下到上进行
稳定性
- 稳定的
时间复杂度
- 最好是 O(n log n)
- 最差也是 O(n log n)
- 所以平均复杂度为 O(n log n)
空间复杂度
- 占用额外空间，线性阶 O(n)

参考

← 经典排序算法-02 经典排序算法-04 →