# 经典排序算法

冒泡排序，选择排序，插入排序

1. 冒泡排序
2. 选择排序
3. 插入排序

# 1. 冒泡排序

冒泡排序(Bubble Sort)是一种简单的排序算法，重复地比较两个相邻元素，如果它们的顺序错误就把它们交换过来，一直重复地进行直到没有再需要交换，这个算法的名字由来是因为越大（小）的元素会经由交换慢慢“浮”到数列的顶端

# 1.1. 算法步骤

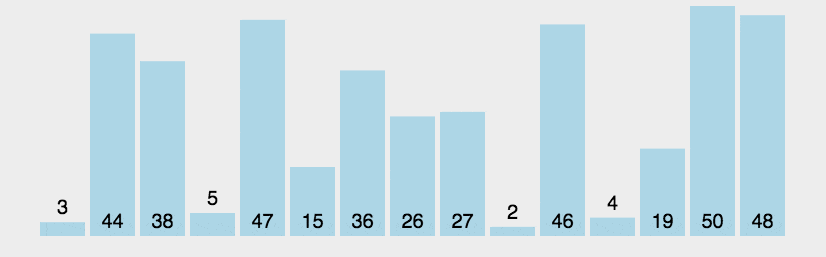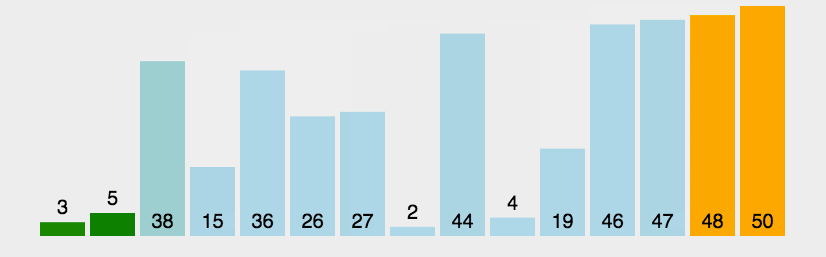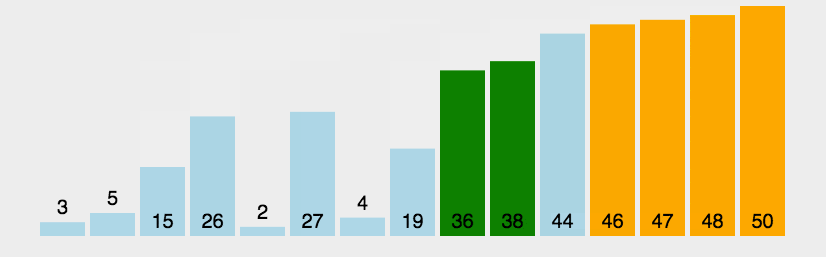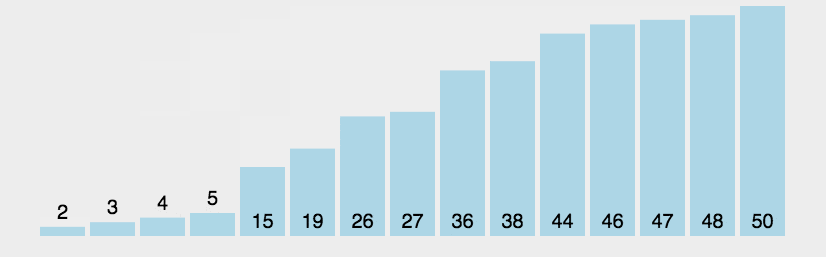
比较相邻的元素，如果第一个比第二个大（小），就交换他们两个
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对
这步做完后，最后的元素会是最大（小）的数
针对所有的元素重复以上的步骤，除了最后一个

# 1.2. 一轮排序

先局部后整体，先写第一轮排序流程是怎么处理的，再考虑整个流程

/**
 * 先写出一轮的冒泡排序处理，冒泡一样的交换位置到最后一位
 *
 * 大于就交换位置是从小到大，每次大于后面的值才交换，最后一位是最大值
 * 小于就交换位置是从大到小，每次小于后面的值才交换，最后一位是最小值
 *
 * array.length - 1，不然会超出边界，因为 array[j + 1]
 *
 * 当然也可以是从j = 1开始，j和j - 1进行比较，这样就不用array.length - 1了
 * 大于和小于也需要调换，大于会变成从大到小，小于会变成从小到大
 * 当然这种逆向的理解起来比较复杂一点，第二块代码是逆向的写法
 *
 * @param array
 */
private static void bubbleSort1(int[] array) {
    print(array);

    for (int j = 0; j < array.length - 1; j++) {
        if (array[j] > array[j + 1]) {
            int temp = array[j];
            array[j] = array[j + 1];
            array[j + 1] = temp;
        }
    }

    /*for (int j = 1; j < array.length; j++) {
        if (array[j] < array[j - 1]) {
            int temp = array[j];
            array[j] = array[j - 1];
            array[j - 1] = temp;
        }
    }*/

    print(array);
}

给定一个数组调用，会发现第一轮结束，最大（小）的数，最大值 9 会浮到最后

public static void main(String[] args) {
    int[] array = {5, 3, 2, 4, 9, 8, 7, 1, 6};
    System.out.println("---------- bubbleSort1 ----------");
    bubbleSort1(Arrays.copyOf(array, array.length));
}

---------- bubbleSort1 ----------
5 3 2 4 9 8 7 1 6 
3 2 4 5 8 7 1 6 9

# 1.3. 基础版本

写好了第一轮排序流程是怎么处理的，直接在外层加上一个循环就搞定了

/**
 * 基于一轮的冒泡排序处理，再增加一个外循环
 * 将每个位置的数字都进行一轮冒泡交换
 * 这样一个最基础的冒泡排序就完成了
 *
 * 给定一个count记录循环次数
 *
 * @param array
 */
private static void bubbleSort2(int[] array) {
    print(array);

    // count记录循环次数
    int count = 0;

    for (int i = 0; i < array.length; i++) {
        for (int j = 0; j < array.length - 1; j++) {
            count++;
            if (array[j] > array[j + 1]) {
                int temp = array[j];
                array[j] = array[j + 1];
                array[j + 1] = temp;
            }
        }
    }
    System.out.println("count: " + count);

    print(array);
}

调用方法，数组排序成功，但是可以看到，循环了 72 次

public static void main(String[] args) {
    int[] array = {5, 3, 2, 4, 9, 8, 7, 1, 6};
    System.out.println("---------- bubbleSort2 ----------");
    bubbleSort2(Arrays.copyOf(array, array.length));
}

---------- bubbleSort2 ----------
5 3 2 4 9 8 7 1 6 
count: 72
1 2 3 4 5 6 7 8 9

# 1.4. 优化版本

基础版本的话，循环了 72 次，这个是可以进行简单优化的，基础版本每个都进行的排序，这是多余的，结尾的就是 i 后面的数字都是已经排序浮动到最后的有序的，可以不用再重复排序

/**
 * 优化版本，内循环减去i就行了
 * 每次冒泡后到i位置的数字都已经排序好了
 * 所以就没必要重复排
 *
 * 可以看到count次数少了一半
 *
 * @param array
 */
private static void bubbleSort3(int[] array) {
    print(array);

    // count记录循环次数
    int count = 0;

    for (int i = 0; i < array.length; i++) {
        for (int j = 0; j < array.length - i - 1; j++) {
            if (array[j] > array[j + 1]) {
                int temp = array[j];
                array[j] = array[j + 1];
                array[j + 1] = temp;
            }
            count++;
        }
    }

    // 还有一种外循环i反过来循环的，意思差不多，就是逆向的
    /*for (int i = array.length - 1; i > 0 ; i--) {
        for (int j = 0; j < i; j++) {
            count++;
            if (array[j] > array[j + 1]) {
                int temp = array[j];
                array[j] = array[j + 1];
                array[j + 1] = temp;
            }
        }
    }*/
    System.out.println("count: " + count);

    print(array);
}

调用方法，数组排序成功，可以看到 count 次数少了一半，变成 36 次

public static void main(String[] args) {
    int[] array = {5, 3, 2, 4, 9, 8, 7, 1, 6};
    System.out.println("---------- bubbleSort3 ----------");
    bubbleSort3(Arrays.copyOf(array, array.length));
}

---------- bubbleSort3 ----------
5 3 2 4 9 8 7 1 6 
count: 36
1 2 3 4 5 6 7 8 9

# 1.5. 优化版本v2

还有一种优化算法，就是立一个 flag，当在一趟序列遍历中元素没有发生交换，则证明该序列已经有序，可以直接结束，但这种改进对于提升性能来说并没有什么太大作用

/**
* 优化版本v2，假定数组某些数已经有序
* 在每轮交换处理可以定一个标记，如果这轮比较都没有交换位置的话
* 说明数据已经有序，可以直接结束
*
* 给定一个count记录循环次数
* 换一个存在某些数有序的数组，可以看到count次数又会变少
*
* @param array
*/
private static void bubbleSort4(int[] array) {
    print(array);

    // count记录循环次数
    int count = 0;

    for (int i = 0; i < array.length; i++) {
        // 设定一个标记
        boolean mark = Boolean.TRUE;

        for (int j = 0; j < array.length - i - 1; j++) {
            if (array[j] > array[j + 1]) {
                int temp = array[j];
                array[j] = array[j + 1];
                array[j + 1] = temp;
                mark = Boolean.FALSE;
            }
            count++;
        }

        // 若为true，则表示此次循环没有进行交换
        if (mark) {
            // 也就是待排序列已经有序，排序已经完成，直接结束
            break;
        }
    }

    System.out.println("count: " + count);

    print(array);
}

换一个存在某些数有序的数组，可以看到 count 次数又会变少，减少到 26 次

public static void main(String[] args) {
    // int[] array = {5, 3, 2, 4, 9, 8, 7, 1, 6};
    System.out.println("---------- bubbleSort4 ----------");
    int[] array4 = {4, 1, 2, 3, 9, 8, 7, 5, 6};
    bubbleSort4(Arrays.copyOf(array4, array.length));
}

---------- bubbleSort4 ----------
4 1 2 3 9 8 7 5 6 
count: 26
1 2 3 4 5 6 7 8 9

# 1.6. 算法总结

描述
- 无序区，有序区
- 从无序区通过交换找到最大（小）元素放到有序区前端
稳定性
- 稳定的
时间复杂度
- 最好应该是线性阶 O(n)
- 最差每次就进行排序为平方阶 O(n^2)
- 所以平均复杂度为平方阶 O(n^2)
空间复杂度
- 没有占用额外空间，所以为常数阶 O(1)

# 2. 选择排序

选择排序(Selection Sort)是一种简单的排序算法，每一次从待排序的数据元素中选出最小（大）的一个元素，存放在序列的起始（末尾）位置，直到全部待排序的数据元素排完

# 2.1. 算法步骤

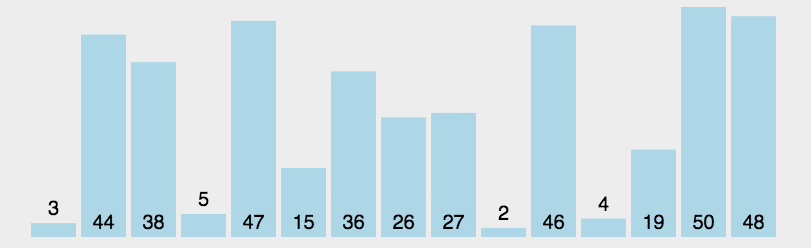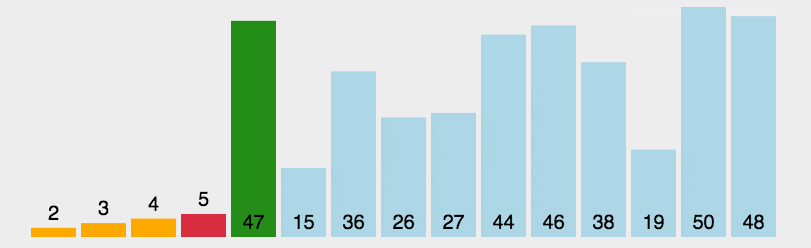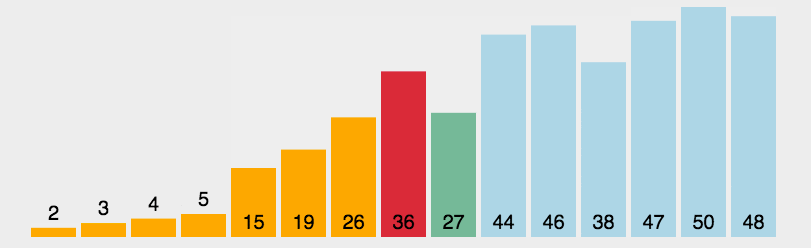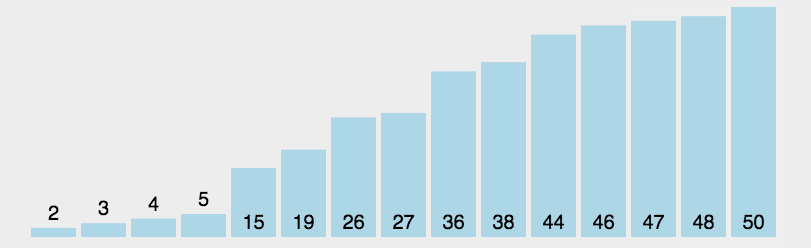
直接在未排序序列中找到最小（大）元素的下标，然后和起始元素交换，再找下一个最小（大）元素的下标交换，以此类推

首先在未排序序列中找到最小（大）元素，存放到已排序序列的起始位置
再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的下一个位置
重复第二步，直到所有元素均排序完毕

优化加强版本

可以同时在未排序序列中寻找最小元素和最大元素，最小元素存放到已排序序列的起始位置，最大元素存放到已排序序列的最终位置

# 2.2. 一轮排序

先局部后整体，先写第一轮排序流程是怎么处理的，再考虑整个流程

/**
 * 先写出一轮的选择排序处理
 *
 * 可以看到最小的数字交换到第一个了
 *
 * @param array
 */
private static void selectionSort1(int[] array) {
    print(array);

    // 记录最小下标位置
    int minIndex = 0;

    for (int j = 0; j < array.length; j++) {
        if (array[j] < array[minIndex]) {
            minIndex = j;
        }
    }

    // 将最小下标值进行交换
    int temp = array[0];
    array[0] = array[minIndex];
    array[minIndex] = temp;

    print(array);
}

给定一个数组调用，可以看到最小的数字 1 交换到第一个了

public static void main(String[] args) {
    int[] array = {5, 3, 2, 4, 9, 8, 7, 1, 6};
    System.out.println("---------- selectionSort1 ----------");
    selectionSort1(Arrays.copyOf(array, array.length));
}

---------- selectionSort1 ----------
5 3 2 4 9 8 7 1 6 
1 3 2 4 9 8 7 5 6

# 2.3. 基础版本

写好了第一轮排序流程是怎么处理的，直接在外层加上一个循环就搞定了

/**
 * 基于一轮的选择排序处理，再增加一个外循环
 * 将每个位置的数字都进行一轮选择交换
 * 这样一个最基础的选择排序就完成了
 *
 * @param array
 */
private static void selectionSort2(int[] array) {
    print(array);

    // count记录循环次数
    int count = 0;

    for (int i = 0; i < array.length; i++) {
        // 记录最小下标位置
        int minIndex = i;

        for (int j = i; j < array.length; j++) {
            count++;
            if (array[j] < array[minIndex]) {
                minIndex = j;
            }
        }

        // 将最小下标值进行交换
        int temp = array[i];
        array[i] = array[minIndex];
        array[minIndex] = temp;
    }

    System.out.println("count: " + count);

    print(array);
}

给定一个数组输出，排序成功

public static void main(String[] args) {
    int[] array = {5, 3, 2, 4, 9, 8, 7, 1, 6};
    System.out.println("---------- selectionSort2 ----------");
    selectionSort2(Arrays.copyOf(array, array.length));
}

---------- selectionSort2 ----------
5 3 2 4 9 8 7 1 6 
count: 45
1 2 3 4 5 6 7 8 9

# 2.4. 优化版本

边界处理优化，j 应该从 j = i + 1，外循环也应该 i < array.length - 1

/**
 * 优化版本，边界处理优化
 *
 * 应该从 j = i + 1 开始，i为0时，如果j = i
 * 那就是array[0]和array[0]比较了一次
 *
 * 外循环也应该i < array.length - 1，也是一样
 * 不进行-1的话结尾array[8]和array[8]多比较了一次
 *
 * @param array
 */
private static void selectionSort3(int[] array) {
    print(array);

    // count记录循环次数
    int count = 0;

    for (int i = 0; i < array.length - 1; i++) {
        // 记录最小下标位置
        int minIndex = i;

        for (int j = i + 1; j < array.length; j++) {
            if (array[j] < array[minIndex]) {
                minIndex = j;
            }
            count++;
        }

        // 将最小下标值进行交换
        int temp = array[i];
        array[i] = array[minIndex];
        array[minIndex] = temp;
    }

    System.out.println("count: " + count);

    print(array);
}

给定一个数组输出，排序成功，count 减少到 36

public static void main(String[] args) {
    int[] array = {5, 3, 2, 4, 9, 8, 7, 1, 6};
    System.out.println("---------- selectionSort3 ----------");
    selectionSort3(Arrays.copyOf(array, array.length));
}

---------- selectionSort3 ----------
5 3 2 4 9 8 7 1 6 
count: 36
1 2 3 4 5 6 7 8 9

# 2.5. 优化版本v2

交换可以优化，如果下标是一样的，说明当前数就是最小的，没必要自己和自己交换了

/**
 * 优化版本v2，交换可以优化，不是每次都需要交换
 *
 * 如果下标是一样的，说明当前数就是最小的
 * 没必要自己和自己交换了
 *
 * @param array
 */
private static void selectionSort4(int[] array) {
    print(array);

    // count记录循环次数
    int count = 0;

    for (int i = 0; i < array.length - 1; i++) {
        // 记录最小下标位置
        int minIndex = i;

        for (int j = i + 1; j < array.length; j++) {
            if (array[j] < array[minIndex]) {
                minIndex = j;
            }
            count++;
        }

        // 最小下标位置和i不相等说明找到新的最小数才进行交换
        if (minIndex != i) {
            int temp = array[i];
            array[i] = array[minIndex];
            array[minIndex] = temp;
        }
    }

    System.out.println("count: " + count);

    print(array);
}

给定一个数组输出，排序成功，不会每次都再进行交换

public static void main(String[] args) {
    int[] array = {5, 3, 2, 4, 9, 8, 7, 1, 6};
    System.out.println("---------- selectionSort4 ----------");
    selectionSort4(Arrays.copyOf(array, array.length));
}

---------- selectionSort4 ----------
5 3 2 4 9 8 7 1 6 
count: 36
1 2 3 4 5 6 7 8 9

# 2.6. 优化版本v3

可以同时在未排序序列中寻找最小元素和最大元素，最小元素存放到已排序序列的起始位置，最大元素存放到已排序序列的最终位置

待补充

# 2.7. 算法总结

描述
- 无序区，有序区
- 从无序区找到最大（小）元素跟到有序区的后面，对数组比较多，交换少
稳定性
- 数组是不稳定的排序方法
- 比如序列 [5， 5， 3] 第一次就将第一个 [5] 与 [3] 交换，导致第一个 5 挪动到第二个 5 后面
- 链表是稳定的吗？
时间复杂度
- 最好是平方阶 O(n^2)
- 最差也是为平方阶 O(n^2)
- 所以平均复杂度为平方阶 O(n^2)
空间复杂度
- 没有占用额外空间，所以为常数阶 O(1)

# 3. 插入排序

插入排序(Insertion Sort)的实现虽然没有冒泡排序和选择排序那么简单，但它的原理应该是最容易理解的了

扑克牌排序，玩过扑克牌的人都能理解
队伍排队，从前往后、按高矮顺序排序

原理简单或许你认为它的实现、次数也很简单，但事实你这么想错了，计算机每次只能进行一次计算，所以每个要确定要插入到那，必须一个一个往前比较

# 3.1. 算法步骤

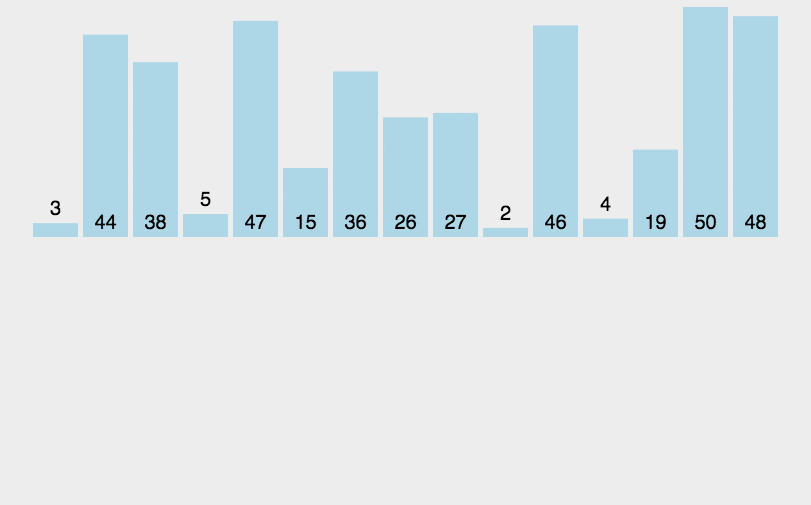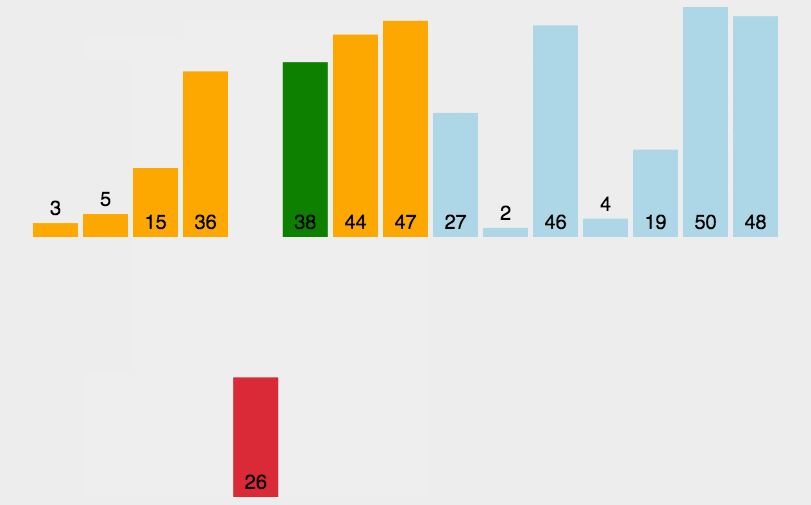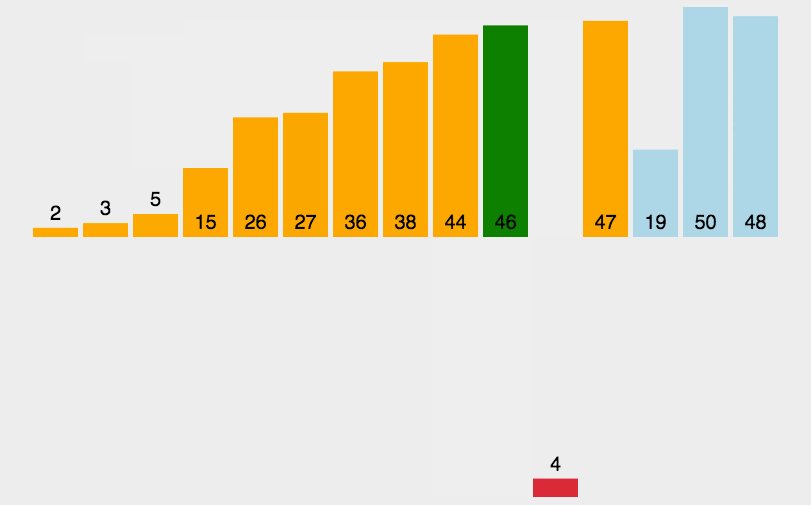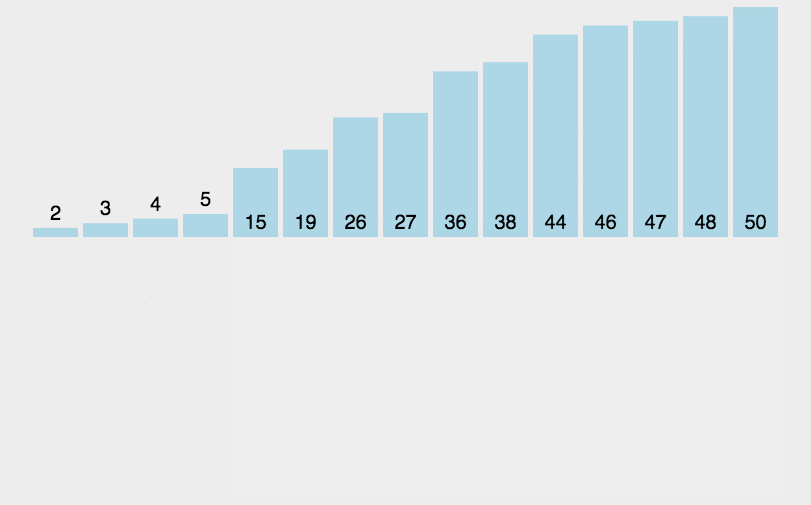
对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入

将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列
从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置
如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面

优化加强版本

希尔排序、拆半插入(二分法拆入)

# 3.2. 一轮排序

先局部后整体，先写第一轮排序流程是怎么处理的，再考虑整个流程

/**
 * 先写出一轮的插入插入处理
 *
 * 设定是从第2个数往前插入
 *
 * @param array
 */
private static void insertionSort1(int[] array) {
    print(array);

    int current = array[2];

    // 从第2个开始比较，没有小于的数据后结束循环进行插入
    int j = 2;
    while (j > 0 && (current < array[j - 1])) {
        array[j] = array[j - 1];
        j--;
    }

    // j不等于2，说明找到了比其小的数，才进行插入
    if (j != 2) {
        array[j] = current;
    }

    // 使用交换的方式
    /*for (int j = 2; j > 0; j--) {
        if (array[j] < array[j - 1]) {
            int temp = array[j];
            array[j] = array[j - 1];
            array[j - 1] = temp;
        }
    }*/

    print(array);
}

给定一个数组输出，可以看到第二个数插入到了小于它数的前面

public static void main(String[] args) {
    int[] array = {5, 3, 2, 4, 9, 8, 7, 1, 6};
    System.out.println("---------- insertionSort1 ----------");
    insertionSort1(Arrays.copyOf(array, array.length));
}

---------- insertionSort1 ----------
5 3 2 4 9 8 7 1 6 
2 5 3 4 9 8 7 1 6

# 3.2. 基础版本

写好了第一轮排序流程是怎么处理的，直接在外层加上一个循环就搞定了

/**
 * 基于一轮的插入排序处理，再增加一个外循环
 *
 * 这样一个最基础的插入排序就完成了
 *
 * @param array
 */
private static void insertionSort2(int[] array) {
    print(array);

    for (int i = 0; i < array.length; i++) {
        int current = array[i];

        // 从后往前的开始比较，没有小于的数据后结束循环进行插入
        int j = i;
        while (j > 0 && (current < array[j - 1])) {
            array[j] = array[j - 1];
            j--;
        }

        // j和i不一致说明找到了比其小的数，才进行插入
        if (j != i) {
            array[j] = current;
        }
    }

    // 使用交换的方式
    /*for (int i = 0; i < array.length; i++) {
        for (int j = i + 1; j > 0; j--) {
            if (array[j] < array[j - 1]) {
                int temp = array[j];
                array[j] = array[j - 1];
                array[j - 1] = temp;
            }
        }
    }*/

    print(array);
}

给定一个数组输出，可以看到排序成功

public static void main(String[] args) {
    int[] array = {5, 3, 2, 4, 9, 8, 7, 1, 6};
    System.out.println("---------- insertionSort2 ----------");
    insertionSort2(Arrays.copyOf(array, array.length));
}

---------- insertionSort2 ----------
5 3 2 4 9 8 7 1 6 
1 2 3 4 5 6 7 8 9

# 3.3. 优化版本

边界处理，外循环可以直接从 1 开始，插入第一个元素无需比较

/**
 * 优化版本，边界处理
 * i可以直接从1开始，0的只有一个元素无需处理
 *
 * 交换的方式的话，优化i < array.length - 1
 *
 * @param array
 */
private static void insertionSort3(int[] array) {
    print(array);

    // 从下标为1的元素开始选择合适的位置插入，因为下标为0的只有一个元素无需处理
    for (int i = 1; i < array.length; i++) {
        int current = array[i];

        // 从后往前的开始比较，没有小于的数据后结束循环进行插入
        int j = i;
        while (j > 0 && (current < array[j - 1])) {
            array[j] = array[j - 1];
            j--;
        }

        // j和i不一致说明找到了比其小的数，才进行插入
        if (j != i) {
            array[j] = current;
        }
    }

    // 使用交换的方式
    /*for (int i = 0; i < array.length - 1; i++) {
        for (int j = i + 1; j > 0; j--) {
            if (array[j] < array[j - 1]) {
                int temp = array[j];
                array[j] = array[j - 1];
                array[j - 1] = temp;
            }
        }
    }*/

    print(array);
}

给定一个数组输出，可以看到排序成功

public static void main(String[] args) {
    int[] array = {5, 3, 2, 4, 9, 8, 7, 1, 6};
    System.out.println("---------- insertionSort3 ----------");
    insertionSort3(Arrays.copyOf(array, array.length));
}

---------- insertionSort3 ----------
5 3 2 4 9 8 7 1 6 
1 2 3 4 5 6 7 8 9

# 3.4. 拆半插入

拆半插入(二分法拆入)

待补充

【排序】(折半)插入排序、希尔排序 (opens new window)

# 3.5. 算法总结

描述
- 无序区，有序区
- 把无序区的元素插入到有序区合适的位置，对数组比较少，交换多
稳定性
- 稳定的
时间复杂度
- 最好是线性阶 O(n)
- 最差为平方阶 O(n^2)
- 所以平均复杂度为平方阶 O(n^2)
空间复杂度
- 没有占用额外空间，所以为常数阶 O(1)

参考

← 经典排序算法-01 经典排序算法-03 →